圆的反演
老板让搞的很偏的知识。这应该是MO的考点吧……OI里面似乎没有出现过这样的题,ACM里倒是出过几道。
讲几何竟然不画图
自己去找个软件画啊,GeoGebra滋瓷在线是坠吼的
首先肯定要讲反演是什么:
给定圆$C$,圆心为$O$,半径为$r$。如果$P$和$P’$在过圆心$O$的直线上,且$|OP||OP’|=r^2 $,那么称$P$与$P’$互为反演。
一般认为$OP$与$OP’$同向。注意到圆$C$的半径只起到一个度量的作用,所以一般也可以不画出反演圆,而是给出反演中心和反演半径。
注意到这里有乘积的形式,一般可以通过移项之后转为相似三角形问题,这在结论的证明中有体现。
称一个图形反演后得到的图形是它的反形。
有以下很显然的小结论:
1.反演关系是对称的,即关于反演圆$C$,如果$P$是$P’$的反演点,那么$P’$也是$P$的反演点。
2.反演圆上的点反演后保持在原处;圆外的点反演后变换为圆内的点;圆内的点反演后变换为圆外的点。
下面的结论比较重要:
1.一条不过反演中心的直线,反形是一个过反演中心的圆;(由反演的对称性)一个过反演中心的圆,反形是一条不过反演中心的直线。
把圆变为直线可能会大大降低题目难度。
2.一个不过反演中心的圆,反形也是一个不过反演中心的圆。反演中心是它们的位似中心,任一对反演点互为逆对应点
3.两个图形存在相切关系,那么反演后仍然满足相切关系。(特别地,如果以两圆切点作为反演中心,那么反演后的两条直线平行)
(这个结论存在更一般的形式)
上面两条结论分别也称作反演的保圆性、保角性。
以上结论的证明看这里:
https://wenku.baidu.com/view/70dbe99404a1b0717fd5dda7.html
那么反演有什么用呢?下面以三道题为例讲解。
hdu 6097 Mindis
题目大意:
给定一个圆心在原点处的圆$C$,给定不在圆外的两点$P,Q$,使得$OP=OQ$。求$C$上一点$D$,使得$DP+DQ$最小。
共有$500000$组询问,$P,Q$横纵坐标绝对值不超过$100$,$C$的半径不超过$100$。
询问有点多,不知道模拟退火能不能过
首先特判掉两种情况:
1.两个点都在圆$C$上:$D$只要与$P$或$Q$重合就好了,直接输出$|PQ|$。
2.两个点与圆心重合,这个时候怎么取答案都会是$2r$。
考虑一般的情况。作出$P,Q$关于圆$C$的反演点$P’,Q’$。任取圆上且不在$OP‘$上的一点$D$,发现有$\triangle OPD\sim \triangle ODP’$,那么有$\frac{DP}{OP}=\frac{DP’}{OD}$,得到$DP’=\frac{r}{OP}DP$,同理可得$DQ’=\frac{r}{OQ}DQ$,所以最小化$DP+DQ$可以转换为最小化$DP’+DQ’$,而$P’$和$Q’$的中垂线是过$O$的。
因此,当$P’Q’$与圆$C$有交时,直接输出$|PQ|$。
否则,最优的$D$是$P’Q’$中垂线与圆$C$靠近直线的交点。这个怎么证明?
由对称性显然
把$P’Q’$中点看成椭圆的中心,$P’,Q’$分别是椭圆的两个焦点,$P’Q’=2c$,而$DP’+DQ’$就是$2a$。由于$c$是定值,$a^2=b^2+c^2$,要使$2a$最小,那么$b$也要最小,显然$b$在$D$为$P’Q’$中垂线与圆$C$靠近直线的交点时取到最小值。
1 |
|
hdu 6158 The Designer
题目大意:
给出两个内切的圆的半径,在两圆之间的部分放小圆,具体关系见下图。求前$N$个圆的总面积。有$t\leq 1200$组测试数据,每组数据$N\leq 10^7$,大圆半径$R\leq100$
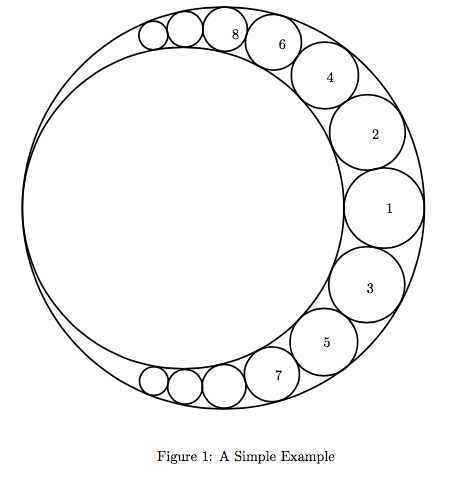
将整个图形以两个大圆的切点为反演中心,任意长为半径反演,那么两个大圆就变成了两条平行直线,小圆就变成了若干个大小相等的、与两条直线相切、相邻两个相切的圆。把图划出来之后就可以利用反演的比例关系很简单地计算出小圆的半径,进而计算出面积了。
注意到这里的$N$非常大,但是$R$比较小,当$N$大到一定程度时,小圆的面积将会非常小,对答案的贡献可以忽略不计,这时结束讨论即可。
1 |
|
hdu 4773 Problem of Apollonius
题目大意:
给定两个相离的圆$C_1,C_2$,给定一个点$P$,求出所有满足下面条件的圆$C$:$C$过点$P$,且与$C_1,C_2$都外切。
共有$T\leq 200$组测试数据,坐标都是正整数,大小不超过$100$。
首先容易想到设出$C$的圆心和半径暴力解方程。但是立即发现这个方程不好解。
考虑反演,假设我们已经拿到了最后的答案,以$P$为反演中心,任意长为反演半径反演之后,$C_1,C_2$仍然是两个圆,而$C$就变换为了一条直线,而这条直线将与$C_1,C_2$都相切,也就是$C_1,C_2$的公切线。
所以大体思路是:将$C_1,C_2$反演后,求出$C_1,C_2$的公切线,再将公切线反演成圆即可。
然而这样做有一个很大的问题:并没有满足圆与$C_1,C_2$外切。这时候有两种想法:
1.把所有公切线求出来之后再检验。但是求两圆的所有公切线略显繁琐,判断虽然简单,但是可能会出现较大的精度差(反演了两次,外加求公切线调用三角函数)。不知道能不能过。
2.观察性质,发现当且仅当$C_1,C_2$反演后的圆心、反演中心$P$在公切线同侧时,$C$与$C_1,C_2$都外切。这样就只需要考虑两圆同侧的公切线,再检验一下就行了。
但是为什么呢?
假设$C_1$与$C$内切,记$C$反演后得到的直线为$l$。显然有这样的结论:$C$内部的点在反演后一定与$C$在$l$的异侧(那么与$P$也是在异侧)。由于$C_1$与$C_2$是相离的,要使$C$与$C_1,C_2$都相切,那么这时$C_1$一定被$C$所包含。那么$C_1$的圆心在$C$的内部,反演后一定与$P$在$l$的异侧,证毕。
求圆和直线的反演画画图,利用反演的关系就很好做了,具体可以参考这篇博客:https://blog.csdn.net/acdreamers/article/details/16966369
代码写得极丑。
1 |
|