CQOI2010 鼹鼠

问题描述

Hilbert鼹鼠住在Hilbert地洞里——地洞的边界是一条n阶Hilbert曲线Hn。Hilbert曲线的定义如下：H1是一个上端缺口的单位正方形；Hn由四份Hn-1组成，其中左下和右下两份没有任何变化，而左上的那一份逆时针旋转了90度，而右上的那一份顺时针旋转了90度。这四份Hn-1用三条单位长度的线段连接起来构成了Hn。H1~H4如下图所示：

　你想捉一只Hilbert鼹鼠来玩，所以往地洞里使劲倒水想把它们赶出来。不过，由于地洞里有空气，无论你怎么倒水，有些地方总是淹不到的（假设水和空气都不可压缩）。输入Hilbert曲线的阶数n和地面的倾斜角α，你的任务是计算能淹没到的面积。

注意，只有当水位严格高于一个障碍物时，水才能越过它往下流。更多细节可以参考下面的例子

输入格式

输入仅包含两个整数n，α。

输出格式

输出仅一行，即被淹没的面积，输出保留小数点后6位。

样例输入

样例输入1：
5 30
样例输入2：
3 45
样例输入3：
4 10
样例输入4：
3 0

样例输出

样例输出1：
190.803848
样例输出2：
15.500000
样例输出3：
91.573592
样例输出4：
26.000000

数据范围

$n\leq 12,α \in [0,90)$

---

第一眼看上去是一道不可做题：分形十分复杂，灌水也似乎很困难，而且还要计算面积。仔细分析之后发现就是一道初中数学题。

首先解决分形。不难推导出$n$阶的边长是$2^n-1$，那么本题中最长为$2^{12}-1=4095$，可以用数组直接存下分形图。

然后考虑分形的规律，按照题目所述模拟即可。接下来关注从$n$到$n+1$阶具体的变化，即变化后哪些格子是地洞。下面以$2$阶转$3$阶为例：

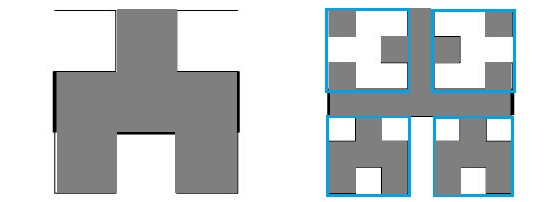
不难发现新的图里，地洞就是左上角、右上角原来不是地洞的部分；左下角、右下角原来就是地洞的部分、最中央的一行和最中央靠上的半列。这样就解决了分形的问题。

再考虑灌水的问题。如何知道一个格子的灌水情况呢？下面使用水面的“基准高度”来描述，“基准高度”指正方形的最下端点到水面的高度，如下图：

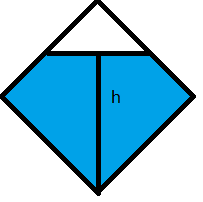
容易看出一个格子的水面基准高度与与之四连通的地洞格子有关。再结合题目条件可知，顶部的一行地洞格子的基准高度一定为$cos\alpha$。

接下来考虑通过顶部的格子推导其他格子的基准高度。首先容易发现最后有水的格子形成了森林，可以把顶部的格子当作根做一次DFS。DFS过程中，考虑四个方向：左上、左下、右上、右下的转移分别会对基准高度产生什么影响，下面以右下转移为例：

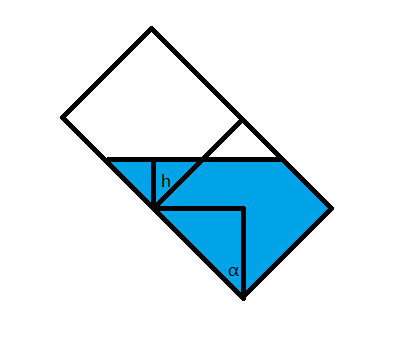
稍微画图就可知右下的基准高度为$h+cos\alpha$。同理可以推出其他转移：右上为$h-sin\alpha$，左上为$h-cos\alpha$，左下为$h+sin\alpha$。同时要注意基准高度的取值范围是$[0,sin\alpha+cos\alpha]$，而且根据题意“只有当水位严格高于一个障碍物时，水才能越过它往下流”，搜到某个位置的基准高度为0就不搜了。

确定了基准高度就可以算面积了，这里就是经典的初中几何问题了= =。根据$h$分成三段讨论计算面积，这里还需要看$\alpha$与$45°$的大小关系，即$cos\alpha$和$\sin\alpha$的大小关系。具体推导就不写了。

注意为了保证精度，将除法部分提到最后。

---

#include<stdio.h>
#include<cmath>
#include<algorithm>
#include<cstring>
#define db double
using namespace std;
const db Pi=atan(1.0)*4.0,eps=1e-10;

int N,alpha,len=1;
bool Map[4100][4100],Tmp[4100][4100],vis[4100][4100];
db Ans,C,S,maxh,ang;

void dfs(int x,int y,db h){
	if(x<1||y<1||x>len||y>len||h<eps||!Map[x][y]||vis[x][y])return;
	vis[x][y]=true;
	if(h>maxh)h=maxh;

	if(alpha==0)Ans+=1;
	else {
		db s=S,c=C;
		if(alpha>45)swap(s,c);
		if(h<=s)Ans+=h*h;
		else if(h<=c)Ans+=(2.0*h-s)*s;
		else Ans+=2.0*s*c-(s+c-h)*(s+c-h);
	}

	dfs(x+1,y,h+C);dfs(x,y+1,h+S);
	dfs(x-1,y,h-C);dfs(x,y-1,h-S);
}

int main(){
	int i,j,k,x,y;
	scanf("%d%d",&N,&alpha);
	Map[1][1]=true;
	for(k=1;k<N;k++){
		for(x=1;x<=len;x++)
		for(y=1;y<=len;y++){
			Tmp[len-y+1][x]=Tmp[y][len+1+ len-x+1]=!Map[x][y];
			Tmp[len+1+x][y]=Tmp[len+1+x][len+1+y]=Map[x][y];
		}
		for(i=1;i<=2*len+1;i++)Tmp[len+1][i]=true;
		for(i=1;i<=len;i++)Tmp[i][len+1]=true;
		len=len*2+1;
		for(i=1;i<=len;i++)
		for(j=1;j<=len;j++)Map[i][j]=Tmp[i][j];
	}
	ang=1.0*Pi*alpha/180;
	C=cos(ang);S=sin(ang);
	maxh=C+S;
	for(i=1;i<=len;i++)dfs(1,i,C);
	if(alpha!=0)Ans=Ans/2.0/S/C;
	printf("%.6lf\n",Ans);
}